在刚刚进入远期合约时,其价值为0。但在进入合约之后,远期合约价值可能为正也可能为负。对银行或其他金融机构来讲,每天计算这些合约的价值是非常重要的(这叫对合约按市场定价)。采用前面引入的符号,假设K是以前成交的合约的交割价格,合约的交割日期是在从今日起T年之后,r是期限为T年的无风险利率,变量F0表示目前的远期价格,即假如在今天成交的话,合约的交割价格。我们还定义f为远期合约今天的价值。
清楚地理解变量F0、K和f的含义是非常重要的。如果今天正好是合约的最初成交日,那么交割价格K等于远期价格F0,而且合约的价值f是0。随着时间的推移,K保持不变(因为它已经被合约确定),但远期价格F0将会变动,而且远期合约的价值f可以变成或正或负。
对于远期合约的多头方(投资资产和消费资产),合约的价值是
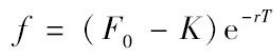 (5-4)
(5-4)
为了说明式(5-4)是正确的,我们采用类似于4.7节里关于远期利率合约价格的证明方式。我们用以下形式构造一个组合:(a)以远期价格K在时间T购买标的资产,和(b)以远期价格F0在时间T卖出标的资产。组合中第1个合约在时间T的收益为ST-K,第2个合约的收益为F0-ST,总收益为F0-K。这个数值在今天是已知的。因此交易组合是无风险的,在今天的价值等于在时间收益的贴现值,即(F0-K)e-rT。因为F0是今天进入远期合约时的远期价格,所以按交割价格F0卖出资产的远期合约价值为0,由此可见,具有交割价格K的合约(多头)在今天的价值为(F0-K)e-rT。类似地,以执行价格K卖出资产的远期合约(空头)的价值为(K-F0)e-rT。
例5-4
一个无股息股票上的远期合约多头是在以前成交的。这一远期合约还有6个月到期。无风险利率(连续复利)为10%,股票价格为25美元,远期合约的交割价格为24美元。这时S0=25,r=0.10,T=0.5和K=24。由式(5-1)得出6个月期的远期合约的价格F0为
由式(5-4)可知远期合约的价值为
式(5-4)说明对于一个资产上的远期合约多头定价时,我们可以假定资产在远期合约到期时的价格等于远期价格F0。为了说明这一点,注意在做出这个假设之后,远期合约在T时刻的收益为F0-K,贴现值为(F0-K)e-rT,这与式(5-4)中的f一致。类似地,在对于远期合约空头进行定价时也可以假设远期价格在将来会实现。这与4.7节中的结果类似:对远期利率合约定价时,我们可以假设远期价格在将来会实现。
将式(5-4)与式(5-1)结合,我们可以得出在没有中间收入的资产上的远期合约多头价值为
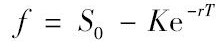 (5-5)
(5-5)
类似地,将式(5-4)与式(5-2)结合,我们可以得出在提供贴现值为I的已知收入的投资资产上远期合约多头价值为
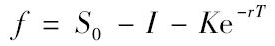 (5-6)
(5-6)
最后,将式(5-4)与式(5-3)并用,我们可以得出提供收益率为q的投资资产上的远期合约多头价值为
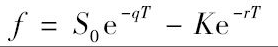 (5-7)
(5-7)
当期货价格变化时,期货合约的盈亏等于其价格变化乘以持有期货头寸的大小。因为期货合约为每日结算,所以收益几乎马上就可以兑现。式(5-4)表示当远期价格变化时,其盈亏等于远期价格变化的贴现值,并乘以其头寸的大小。
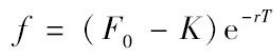 (5-4)
(5-4)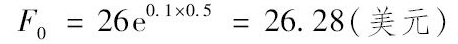
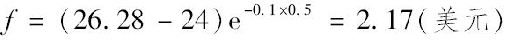
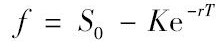 (5-5)
(5-5)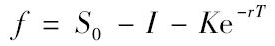 (5-6)
(5-6)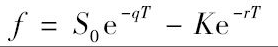 (5-7)
(5-7)