布莱克-舒尔斯模型,简称BS模型,又称布莱克-舒尔斯-墨顿模型,是一种为期权或权证等金融衍生工具定价的数学模型,由美国经济学家迈伦·舒尔斯与费雪·布莱克首先提出,并由罗伯特·墨顿修改模型于有派发股利时亦可使用而更完善。由此模型可以推导出布莱克-舒尔斯公式,并由此公式估算出欧式期权的理论价格。此公式问世后带来了期权市场的繁荣。该公式被广泛使用,虽然在很多情况下被使用者进行一定的改动和修正。很多经验测试表明这个公式足够贴近市场价格,然而也有会出现差异的时候,如著名的“波动率的微笑”。
该模型就是以迈伦·舒尔斯和费雪·布莱克命名的。1997年迈伦·舒尔斯和罗伯特·墨顿凭借该模型获得诺贝尔经济学奖。然而它假设价格的变动,会符合高斯分布(即俗称的钟形曲线),但在财务市场上经常出现符合统计学肥尾现象的事件,这影响此公式的有效性。
B-S模型5个重要假设
金融资产价格服从对数正态分布,即金融资产的对数收益率服从正态分布;
在期权有效期内,无风险利率和金融资产收益变量是恒定的;
市场无摩擦,即不存在税收和交易成本;
金融资产在期权有效期内无红利及其它所得(该假设后被放弃);
该期权是欧式期权,即在期权到期前不可实施。
模型
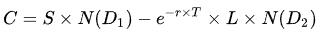
其中:
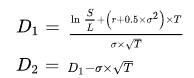
Ln:自然对数;
C:期权初始合理价格;
L:期权交割价格;
S:所交易金融资产现价;
T:期权有效期;
r:连续复利计无风险利率H;
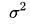 :年度化方差;
:年度化方差;
N():正态分布变量的累积概率分布函数。
派发股利的期权定价模型
布莱克-舒尔斯模型假定在期权有效期内标的股票不派发股利。若派发股利需改用布莱克-舒尔斯-墨顿模型,其公式如下:
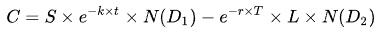
其中:
k:表示标的股票的年股利收益率(假设股利连续支付,而不是离散分期支付)
Ln:自然对数;
C:期权初始合理价格;
L:期权交割价格;
S:所交易金融资产现价;
T:期权有效期;
r:连续复利计无风险利率H;
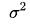 :年度化方差;
:年度化方差;
N():正态分布变量的累积概率分布函数。
股票投资理论和策略
本文由东方铜牛网整理编辑,转载 BS模型_布莱克-舒尔斯模型 请注明文章地址链接。
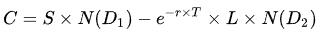
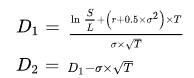
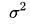 :年度化方差;
:年度化方差;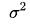 :年度化方差;
:年度化方差;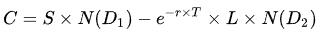
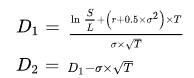
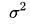 :年度化方差;
:年度化方差;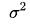 :年度化方差;
:年度化方差; |基本面分析
频道
|基本面分析
频道
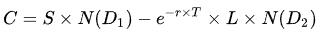
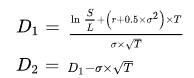
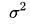 :年度化方差;
:年度化方差;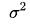 :年度化方差;
:年度化方差;