斜率的计算公式及其在不同领域的应用

斜率，这事儿其实挺简单的

你知道吗？斜率这个词听起来好像很高深的样子，但实际上它就是用来描述一条直线倾斜程度的一个数值。想象一下，如果你站在一个山坡上，这个坡的陡峭程度就可以用斜率来表示了。在数学里头，我们通常会说斜率是两点之间高度变化与水平距离变化的比例。简单来说，就是“上升了多少”除以“走了多远”。

计算公式，跟着我一起念

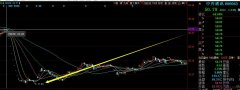
那么，怎么计算斜率呢？别担心，这事儿不难。假设你有两个点A(x1, y1)和B(x2, y2)，想要知道连接这两点的直线有多斜，你就按照下面这个公式来：\[m = \frac{y_2 y_1}{x_2 x_1}\]。这里的\(m\)代表的就是斜率啦！你看，是不是很简单？就像是问你从家到学校的路上，每走一步升高了多少米一样。

生活中的斜率，无处不在

说到斜率的应用，那可真是广泛得很。比如说，在建筑设计中，设计师们需要考虑屋顶或者楼梯的倾斜角度，这时候斜率就派上用场了；又或者是道路规划时，工程师得确保公路的坡度既安全又能有效排水，这里也离不开对斜率的考量。甚至是在经济学领域，通过分析收入与消费之间的关系曲线，经济学家也能利用斜率来预测未来经济走势呢！

教育里的小助手

对于学生朋友们而言，理解斜率的概念不仅有助于解决几何题目，还能帮助大家更好地掌握物理知识。比如学习力的作用效果时，如果能将物体受到的力分解成垂直和平行于地面的分量，那么使用斜率的概念就能更容易地分析出物体运动状态的变化了。这样一来，复杂的物理问题似乎也变得不再那么难以捉摸了吧？

体育竞技中的秘密武器

就连体育界也没放过斜率这一好帮手。运动员训练时，教练可能会根据跑道或游泳池的设计调整训练计划，而这些设计往往都涉及到精确计算不同区域的斜率。此外，在滑雪等冬季项目中，了解雪道的倾斜程度对于提高成绩同样至关重要。可以说，掌握了斜率的知识，就像是给自己的比赛准备了一件隐形的装备呢！

总结一下吧

总而言之，虽然斜率听起来像是个专业术语，但它实际上是我们日常生活中经常会遇到的一个概念。无论是建筑、工程还是教育体育等领域，都能看到它的身影。希望今天聊的内容能够让你对斜率有一个更加全面的认识，并且发现原来数学也可以这么贴近生活哦！

Q&A时间

问：斜率只能用于直线吗？

答：不是的哦，虽然最开始我们讨论的是直线上两点间的斜率，但其实对于曲线来说，我们可以通过求导数来找到某一点处切线的斜率，这样就能研究曲线局部的变化趋势啦。

问：为什么有时候斜率会被称作“梯度”？

答：嗯，这个问题问得好！在某些情况下，特别是在处理多维空间中的函数时，“梯度”这个词更常用一些。它可以看作是多个方向上变化率组成的向量，而在二维平面上，这个概念简化后就变成了我们熟悉的斜率了。

问：除了上面提到的例子外，还有哪些地方会用到斜率呢？

答：哎呀，太多了！比如摄影爱好者调整相机角度时考虑背景与主体之间的相对位置；或者是在音乐制作过程中，调整音轨音量随时间变化的速度等等。只要你留心观察，就会发现斜率真的是无处不在呢！