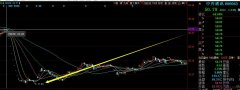
斜率k的计算公式及其在不同领域的应用

斜率k，这东西到底是个啥？

咱们今天聊聊斜率k，听起来挺专业的词儿，其实它就是用来描述一条直线倾斜程度的一个数。想象一下，你站在一个山坡上，如果这个坡特别陡，那它的斜率就大；要是平缓得像公园里的小路，那斜率自然就小了。在数学里头，我们用k来表示这个值，它能帮我们更好地理解图形之间的关系。

斜率k的计算公式，简单到不行

说到怎么算斜率k，其实方法挺简单的。假设你有两个点A(x1, y1)和B(x2, y2)，那么斜率k就可以通过下面这个公式来计算：\[ k = \frac{y_2 y_1}{x_2 x_1} \]。你看，只要知道两点坐标，代入公式一算，斜率就出来了。是不是觉得还挺容易掌握的？不过要注意哦，分母不能为零，否则就无解啦！

斜率k在日常生活中的身影

别以为斜率只是书本上的知识，其实在日常生活中也能见到它的影子。比如开车时遇到的山路，越陡峭的地方，斜率绝对值越大；再比如说建筑设计中，屋顶的设计也需要考虑斜率，以确保雨水能够顺畅流下而不积水。还有，在体育运动中，比如滑雪道的设计，也会根据不同的难度级别调整斜率，让运动员体验不同速度带来的刺激感。

经济学领域里的斜率k

经济学里头，斜率k也有着重要的作用。当我们谈论需求曲线或供给曲线时，斜率可以帮助我们了解价格变化对商品需求量的影响程度。一般来说，如果一条需求曲线比较平坦（斜率较小），说明消费者对于价格变动不太敏感；反之，如果曲线非常陡峭（斜率较大），则表明即使是很小的价格波动也可能导致需求量大幅下降。这种分析对于制定合理的定价策略非常重要。

物理学中的斜率k

物理学里面，斜率k同样扮演着不可或缺的角色。最典型的例子就是在研究物体运动状态时使用的位置时间图。在这个图表上，直线的斜率代表了物体的速度——斜率越大，意味着物体移动得越快。此外，在电学领域，当绘制电压与电流的关系图时，该直线的斜率实际上反映了电路中电阻的大小。这些应用都展示了斜率如何帮助科学家们更直观地理解和解释自然界的现象。

斜率k在工程学的应用

工程师们也经常利用斜率来进行各种设计工作。比如桥梁建设过程中，需要精确计算桥面的倾斜角度以保证结构稳定性和安全性；又或者是在水利工程中，通过对水流路径上各点高度差的测量，可以估算出水流动态特性，进而优化渠道布局。可以说，在很多工程项目背后，都有斜率默默发挥着关键作用呢！

总结一下吧

总之啊，虽然斜率k看起来只是一个小小的数学概念，但它却贯穿于我们生活的方方面面，从最基本的几何学到复杂的科学研究，几乎无处不在。掌握了斜率的知识后，你会发现原来身边那么多看似平常的事物背后都有着深刻的数学原理支撑着。希望这篇文章能让大家对斜率有一个更加全面的认识，并且激发起探索更多有趣知识点的兴趣！

Q&A 时间

问：为什么有时候斜率会是负数？

答：当一条直线从左向右逐渐下降时，它的斜率就会是负数。这是因为此时y随x增加而减少，按照斜率公式计算出来的结果自然也就成了负值。

问：斜率k等于0意味着什么？

答：如果一条直线的斜率为0，那就说明这条线是水平的，即无论x怎样变化，y的值都不会改变。这种情况常见于某些特定条件下的物理现象或是经济模型中。

问：除了上述提到的应用外，斜率k还能用在哪里？

答：其实还有很多其他领域也会用到斜率的概念，比如计算机图形学中处理图像变换、统计学里分析数据趋势等。只要你留心观察，就会发现斜率真是个万能的好帮手！